Exercício C
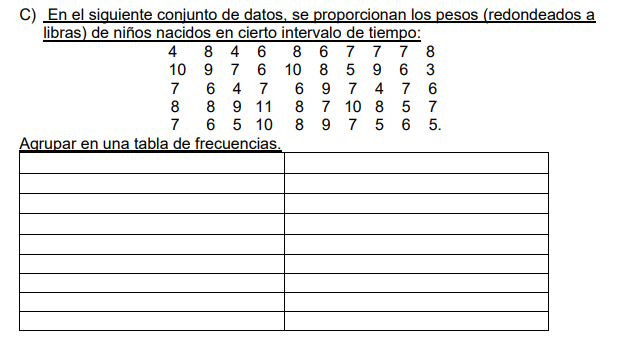
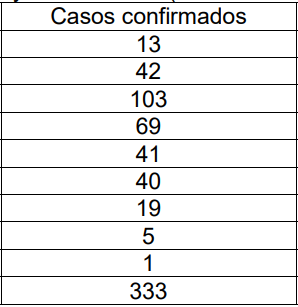
O primeiro passo deve ser a separação de frequência de cada numero e a contagem do numero total de números dessa forma:
(frequência é o numero de vezes que se repete esse dado)
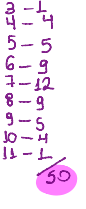
(5 é a quantidade de números que estão na vertical e 10 na horizontal, multiplicando se tem o valor total)

Após confirmar que os números bateram, prossiga com a colocação do título que deve ser referente ao exercício em questão, nesse caso se trata do peso de crianças nascidas num intervalo de tempo, então se coloca assim:

E assim se distribui com os dados que foram analisados acima:
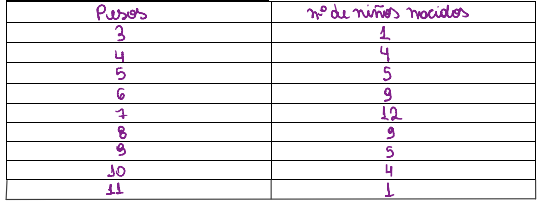
e é só isso.
Exercício D
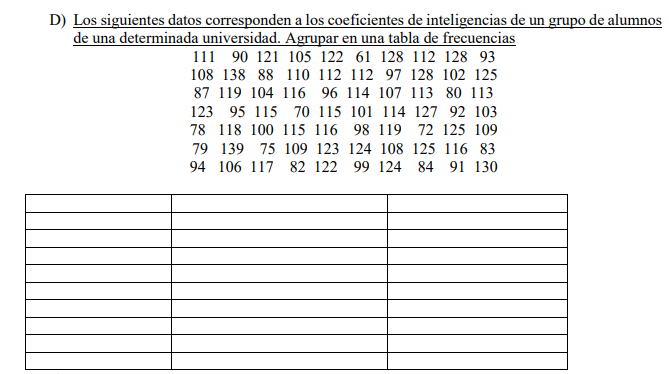
O primeiro passo seria separar os números e as frequências deles dessa forma, e somar a quantidade de frequências que possuem parar ver se bate com o numero total:
(frequência é o numero de vezes que se repete esse dado)

24 + 44 + 2 = 70 (eu separei assim para caber na folha, mas se vc fizer numa linha reta essa parte vc nem faria)
que é exatamente igual ao numero total:

7 x 10 = 70
Com os valores batendo, deve-se prosseguir para descobrir o Rango, Classe e Amplitude, com essas fórmulas e esses resultados:
Rango= maior dado – o menor dado (nesse caso seria o 61 e o 139) = R
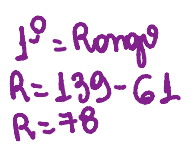
Clase= raiz do numero total (nesse caso o total é 70) = K
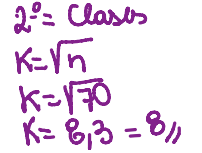
Amplitude= Rango divido pela clase
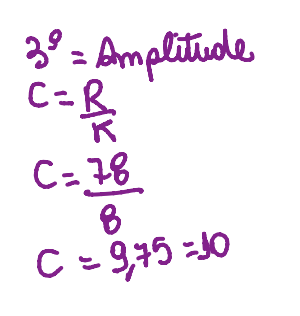
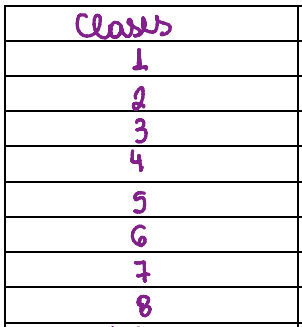
Agora, comece a completar a tabela começando pelos títulos, o 1 quadrado serão as classes, o segundo a amplitude do que se refere o texto em cada classe (Coeficiente de inteligência) e por ultimo a frequência (número de alunos);

Para completar a classe se deve distribuir entre os quadrados o resultado obtido na conta, no caso dessa conta o valor deu 8, então:
O número da amplitude (que vai no meio) deve conter a quantidade de números que foi obtido através do cálculo, nesse caso 10, então se coloca o menor número e a partir dele deve conter 10, o menor número seria 61, para conter 10 números seria do 61 ao 70 pois dentro dessa amplitude contém: 61, 62, 63, 64, 65, 66, 67, 68, 69 e o 70, 10 números, faz o mesmo com os seguintes.

Para finalizar se busca a frequência na quantidade de vezes somadas que esses números aparecem, no 1 caso da primeira fileira do 61 ao 70, aparecem apenas 1x o 61 e 1x o 70, somados então seriam 2, já a segunda fileira do 71 ao 80, aparecem o 72, 75, 78, 79 e 80 1 x cada, somando 5. (faz o mesmo com os seguintes)

e para finalizar a tabela e garantir que está correto o calculo, soma-se o total de frequências (número de alunos, nesse caso) e completa a tabela.

Exercício E
clique aqui: Link do exercício E , eu já havia respondido antes.
Exercício F
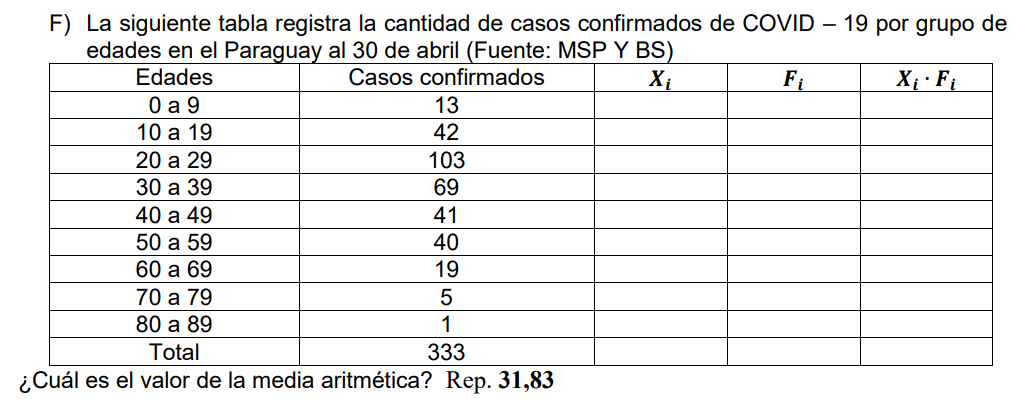
Para completar o ponto médio que é o 𝑋𝑖, vc deve somar os primeiros valores dados e fazer sua média, ou seja, dividir por 2. A primeira idade é 0 e 9 anos, entao o ponto médio seria 9 dividido por 2, no caso 4,5. (o mesmo para o restante)
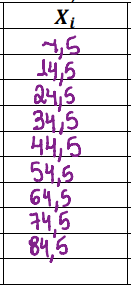
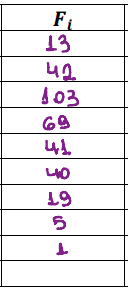
Para completar a frequência que é o Fi, vc deve repetir o 2 dado que se refere a sequência de vezes que o número de idades (nesse caso), se repete.
Ficando assim:
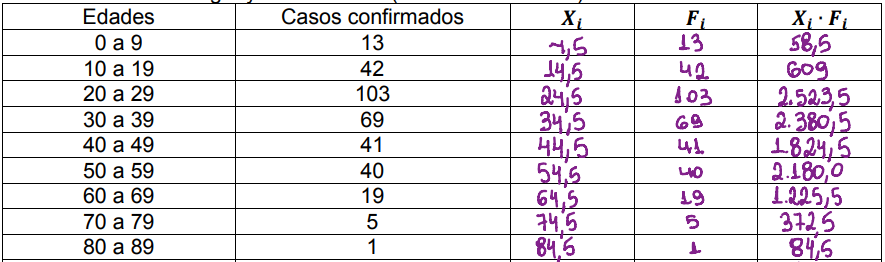
Para o Xi Fi, apenas é feita a multiplicação do 𝑋𝑖 pelo Fi, no primeiro quadrado, seria o 4,5x 13 = 58,5 (os demais seguem o mesmo raciocínio)
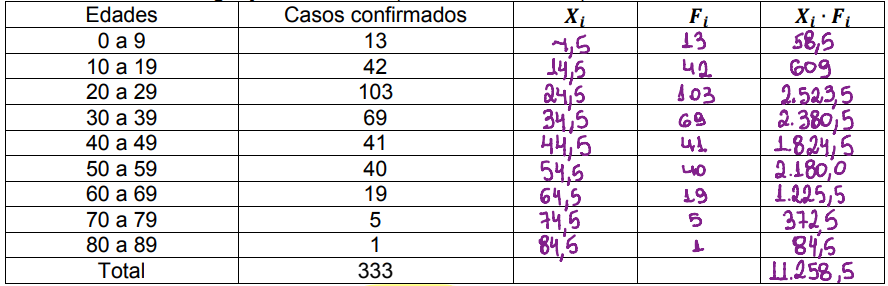
Aí acrescenta-se o total, somando todos os 𝑋𝑖 Fi;
Para descobrir o valor da média se usa essa fórmula:
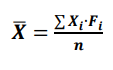
Substituindo os valores fica assim:
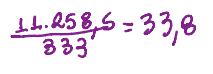
Deve-se fazer a interpretação desse dado, usando média ou promédio na frase.

Ignorem o espanhol e… essa resposta não bateu com a da Dra.
Exercício G

O primeiro passo é identificar a classe modal (a que possui maior frequência, nesse caso a 4 classe pois a 15v é o maior valor)

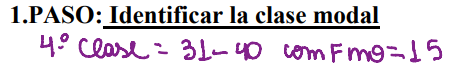
Calcular todos os elementos que serão necessários para aplicar na formula: (todos a partir da clase modal)
Li (Limite real inferior): se é da 4 classe devemos pegar o primeiro número (31) + o anterior a ele (30)e dividir por 2
Ls (Limite real superior): se é da 4 classe devemos pegar o segundo número (40) + o posterior a ele (41) e dividir por 2
O delta 1 e 2 se utiliza o número de frequência como base, nesse caso o 15
O ∆1 diminuiria o 15 com o anterior a ele, nesse caso o 12
O ∆2 diminuiria o 15 com o posterior a ele, nesse caso o 8

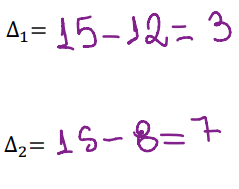
Após encontrar todos os números se aplica essa fórmula:
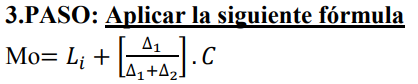
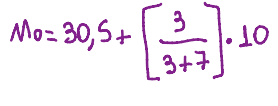
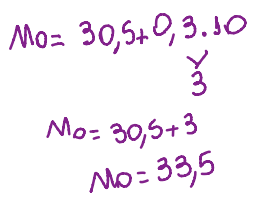
E faz a interpretação baseado no texto, nesse caso se fala sobre tempo.

Exercício h



Começando pelo primeiro item, a média onde vc soma todos os valores do enunciado e divide pela quantidade de números que tem, dessa forma:
52, 43, 30, 38, 30, 42, 12, 46, 39, 37, 34, 46, 32, 18 e 41, dividindo por 15, porque são 15 números.
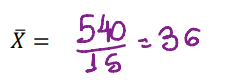
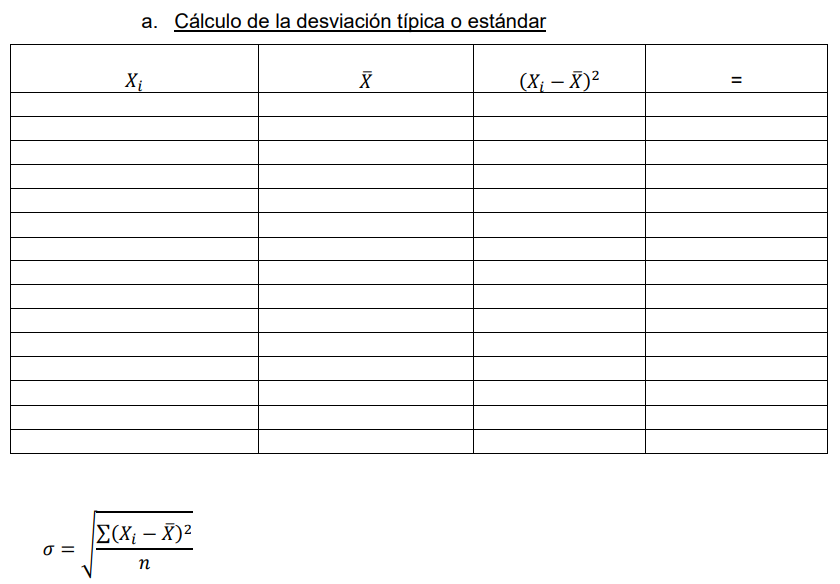
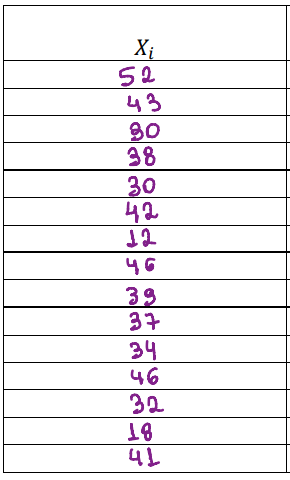
Para completar a tabela de desviación típica primeiro vc distribui todos os números acima, no Xi.
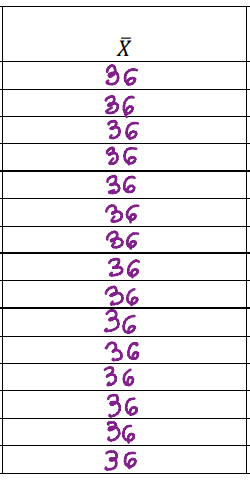
x̅ é a média, então repete o mesmo valor em todos:
O próximo é só substituir os valores nessa fórmula
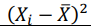
Então de todos seriam esses cálculos:

Na ultima parte da tabela, os resultados desses cálculos:
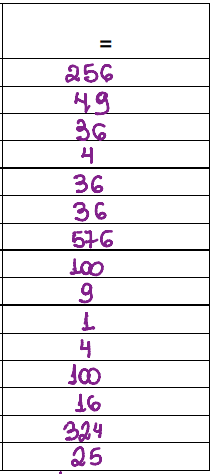
A tabela então fica assim:
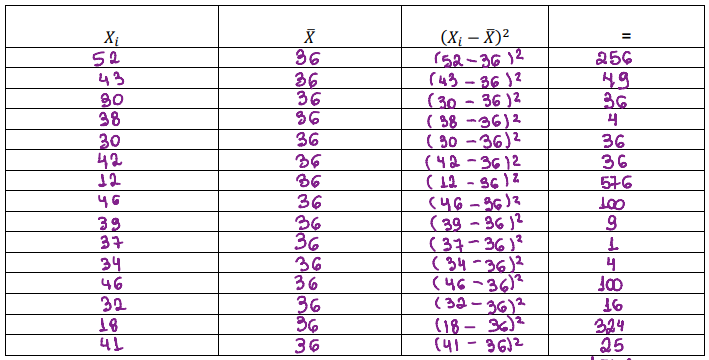
Para calcular a desviación típica se usa essa fórmula:
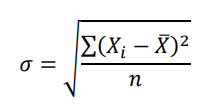
Onde o ∑ representa somatória, então nesse caso , seriam a somatória de todos os valores acima, que nesse caso dá 1572.
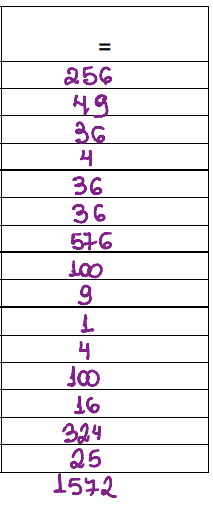
Substituindo esses valores na fórmula:
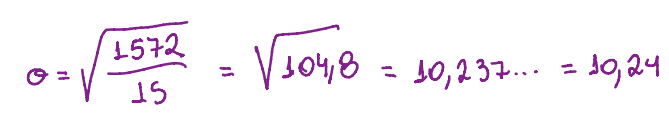
Agora para calcular o coeficiente de variación se usa essa fórmula:
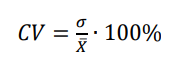
Substituindo na fórmula e calculando obtemos:
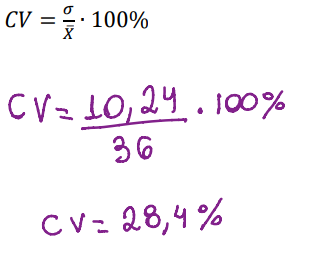
Para de fazer a interpretação desse resultado deve-se gravar esses valores e responder como está em negrito:
0% – 25% No hay dispersión de los datos con relación a la media. La media es altamente representativa.
25,1 – 70% Moderada dispersion. La media es moderadamente representativa
70,1% – 100% Dispersión total de los datos con relación a la media. La media no es representativa.
Nesse caso com o coeficiente de variación se encaixa na moderada dispersion, entre 25,1 – 70%, então a resposta ficaria assim:

Exercício I
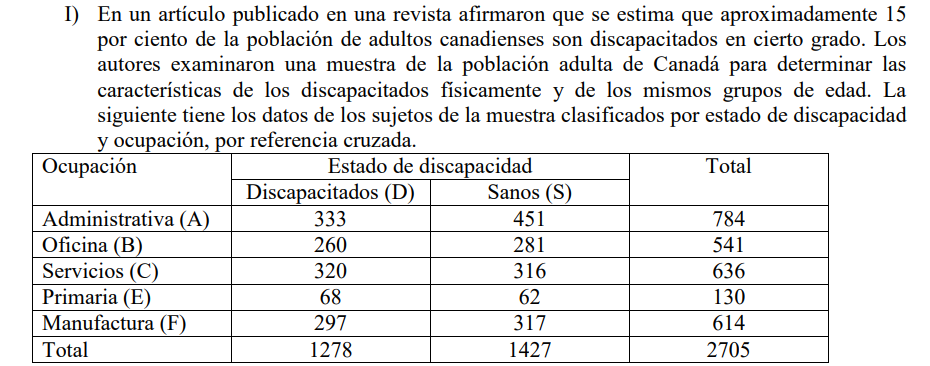

Explicação:

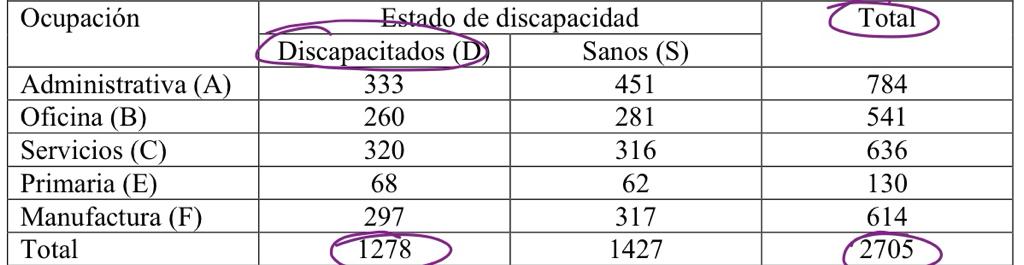
Como nesse caso seria “discapacitada“, deve-se pegar o total de discapacitados e dividir pelo total de pessoas pesquisadas.
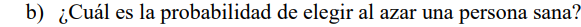
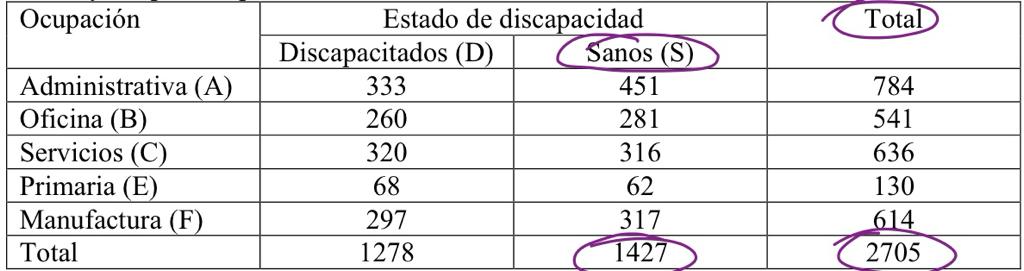
Como nesse caso seria “sanos“, deve-se pegar o total de sanos e dividir pelo total de pessoas pesquisadas

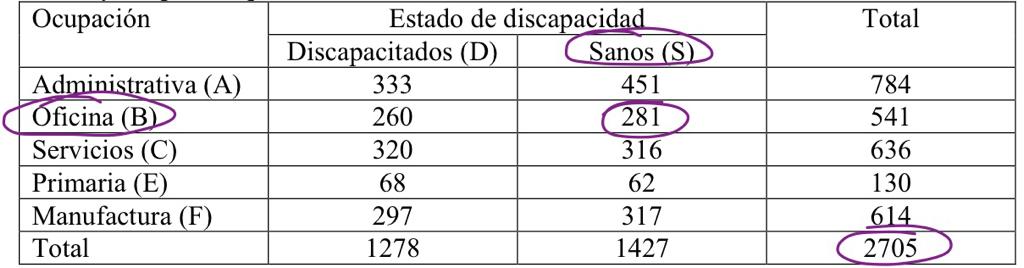
Como nesse caso seria uma pessoa sana e sua ocupação é a oficina , deve-se pegar o total de são sanas e trabalham numa oficina e dividir pelo total de pessoas pesquisadas
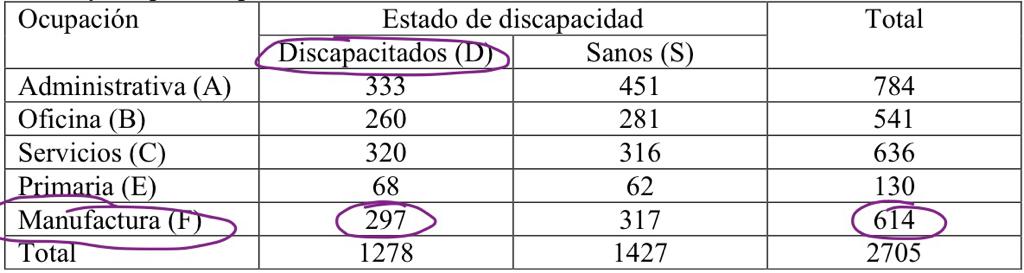
Como nesse caso seria uma pessoa “discapacitada” mas que trabalha na manufatura, deve-se pegar o total de discapacitados que trabalham numa manufatura e dividir pelo total de pessoas que trabalham na manufactura.